
Figure 1 - A sample generated maze using a 50 x 50 grid
Did you ever get the feeling that cubicles were laid out with the idea that there could be no escape? (Must be I am a bit overworked these days). Today's article focuses on how to generate a maze using the depth first search algorithm. This is a very simple but clever algorithm that creates a maze by randomly stripping one available wall between two cells for every cell in the grid. The steps to the algorithm are as follows:
- Pick any random cell in the grid (In this implementation we use the upper left hand corner.)
- Find a random neighboring cell that hasn't been visited yet.
- If you find one, strip the wall between the current cell and the neighboring cell.
- If you don't find one, return to the previous cell.
- Repeat steps 2 and 3 (or steps 2 and 4) for every cell in the grid.
Note: A good place to visit to understand this algorithm is the MazeWorks site.
Having examined the algorithm, I was able to come up with a set of classes that would help me implement it. Below is the design for the Maze Generator Application. The Application allows you to generate a maze of any grid dimension and grid cell size. It also allows you to print and print preview the grid:
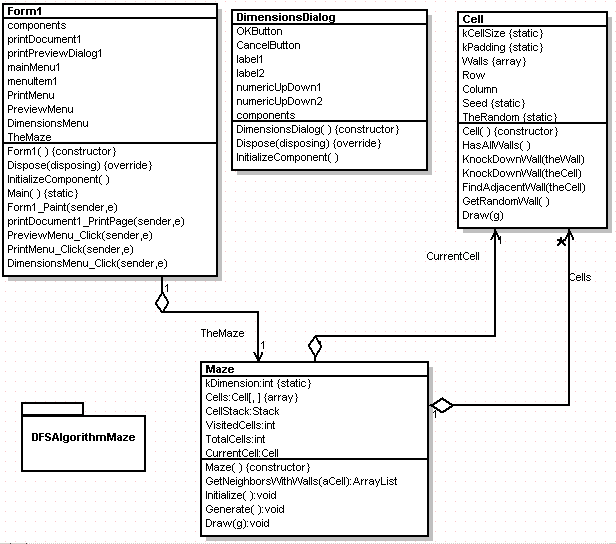
Figure 2 - Maze Generation Application Reverse engineered using the WithClass 2000 UML Tool
As you can see from the UML design, the Maze class generates the maze and contains a collections of Cells to work the algorithm. Each cell contains an array of 4 walls which can be "knocked down" by setting an element in the array to zero. The code for implementing the Depth First Search is shown below. It increments the total number of cells visited in a while loop and completes when the VisitedCells equals the n x n number of grid cells. As stated in the algorithm, first it gets a list of neighboring cells with 4 walls intact and picks one of them at random (if a neighbor exists). It then knocks down a wall between the current cell and the randomly chosen cell. The current cell is pushed onto a stack and the randomly chosen cell becomes the new current cell. If no adjacent neighbors exist with 4 walls intact, the previous cell is popped off the stack and made the current cell.
public void Generate()
{
while (VisitedCells < TotalCells)
{
// get a list of the neighboring cells with all 4 walls intact
ArrayList AdjacentCells = GetNeighborsWithWalls(CurrentCell);
// test if a cell like this exists
if (AdjacentCells.Count > 0)
{
// yes, choose one of them, and knock down the wall between it and the current cell
int randomCell = Cell.TheRandom.Next(0, AdjacentCells.Count);
Cell theCell = ((Cell)AdjacentCells[randomCell]);
CurrentCell.KnockDownWall(theCell);
CellStack.Push(CurrentCell); // push the current cell onto the stack
CurrentCell = theCell; // make the random neighbor the new current cell
VisitedCells++; // increment the # of cells visited
}
else // No adjacent cells that haven't been visited, go back to the previous cell
{
CurrentCell = (Cell)CellStack.Pop();
}
}
}
Conclusion
Mazes are fun to solve, but are also a good background for graphic games. In my next article I'll attempt to combine the eater game with the maze generation. Enjoy some aMazing Puzzles in C# and .NET.