Note: this article is published on 07/20/2024.
I came from science, I have never had a chance to learn or play a game such as an algorithm in my student career. Most algorithm problems I met are in interviews. In my view, these kinds of tricks are just boby level games, but if you did not have related training previously, you might not get the solution immediately. So, I will open a topic, or series, to record the algorithm questions I met or I played previously (10/03/2021, from my first algorithm article).
This series will include,
I will add more on this topic probably from my notes or practice code.
A - Introduction
This article will discuss the algorithm effiency measurement, including time measurement and space measurement, and the Big O notation calculation. This is the structure of this article,
- A - Introduction
- B - Algorithm Efficiency
- C - Measurement of Time Algorithm Efficiency (Complexity)
- D - Measurement of Space Algorithm Efficiency (Complexity)
- E - Big O Notation Calculator
B - Algorithm Efficiency
- Algorithms are measured by their efficiency, defined by time and space complexity.
- Time complexity measures the execution time of an algorithm relative to input size.
- The time complexity of an algorithm quantifies the amount of time taken by an algorithm to run as a function of the length of the input. Note that the time to run is a function of the length of the input and not the actual execution time of the machine on which the algorithm is running on.
- Space complexity tracks the memory usage of an algorithm as the input size grows.
- The space Complexity of an algorithm is the total space taken by the algorithm with respect to the input size. Space complexity includes both Auxiliary space and space used by input.
- Space complexity is a parallel concept to time complexity. If we need to create an array of size n, this will require O(n) space. If we create a two-dimensional array of size n*n, this will require O(n2) space.
- Big O notation helps describe the upper limits of an algorithm’s growth rate.
- Understanding algorithm efficiency involves analyzing and optimizing both time and space complexity.
C - Measurement of Time Algorithm Efficiency (Complexity)
Some common time complexities are:
- O(1): --- Constant time – The algorithm takes the same time regardless of the input size.
- O(log n):--- Logarithmic time – The time grows logarithmically as the input size increases.
- O(n): --- Linear time – The time grows linearly with the input size.
- O(n log n): --- Linearithmic time – The time grows in linear and logarithmic rates.
- O(n^2): --- Quadratic time – The time grows quadratically with the input size.
- O(2^n): --- Exponential time – The time doubles with each additional element in the input.
- O(n!): --- Factorial time – The time grows factorially with the input size.
D - Measurement of Space Algorithm Efficiency (Complexity)
Some common space complexities are:
- O(1): --- Constant space – the algorithm uses a fixed amount of memory regardless of the input size.
- O(n): --- Linear space – the memory usage grows linearly with the input size.
- O(n^2): --- Quadratic space – the memory usage grows quadratically with the input size.
E - Big O Notation Calculator
Some common space complexities are:
Measure for two dimention loop:
for (int i = 0; i < A.Length; i++)
{
P[i] = 1;
for(int j = 0; j < A.Length; j++)
{
if(i != j)
P[i] = P[i]*A[j];
}
}
The results from these two calculators:


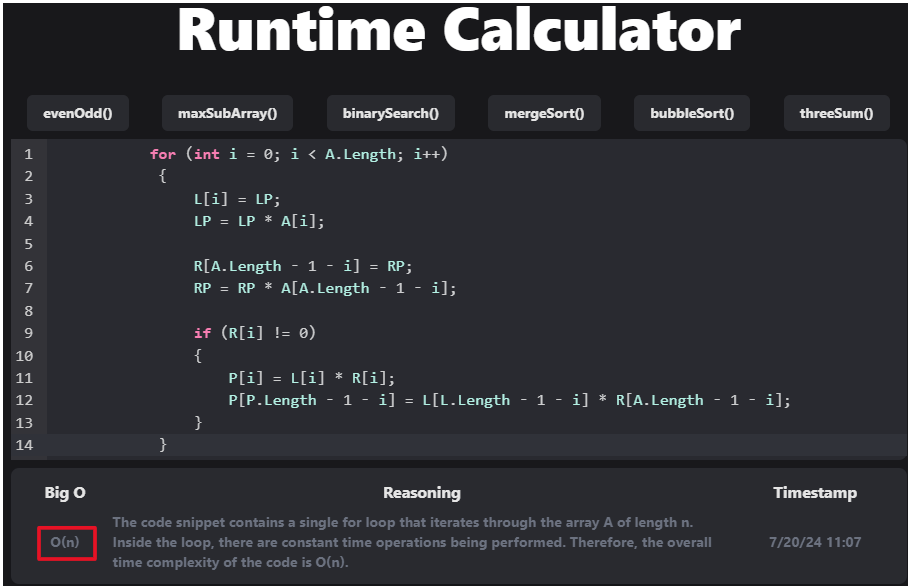
Measure for One dimention loop:
for (int i = 0; i < A.Length; i++)
{
L[i] = LP;
LP = LP * A[i];
R[A.Length - 1 - i] = RP;
RP = RP * A[A.Length - 1 - i];
if (R[i] != 0)
{
P[i] = L[i] * R[i];
P[P.Length - 1 - i] = L[L.Length - 1 - i] * R[A.Length - 1 - i];
}
}
Results:

References:




