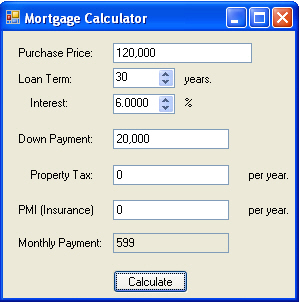
Figure 1 - Mortgage Calculator Form
Many first time home buyers are stumped about how a mortgage works (me included). Say you are buying a $100,000 home at a fixed interest rate of 6% for a 30 year loan. This doesn't mean that you calculate the mortgage as follows: $100,000/(30*12) + ($100,000)*6%/(30*12) as might expect. You are actually paying a lot more. The yearly interest rate is applied fractionally per month and compounded over the life of the mortgage. Therefore, you are paying an interest each month of 6%/12 or about .5% compounded over the length of the loan. Plus, you need to pay property taxes, home owner's insurance, points, and other costs that pop out of the woodwork (so to speak). You actually wind up paying a lot more than $100,000. For a 30 year mortgage at 6% you pay more than two times the cost. With this in mind, how does a bank come up with your payment per month?
Let's first define the variables:
loan: l = $100,000
annual rate: r = 6% (or .06)
period: p = 30 years (or 360 mos.)
monthly payment: x
The total worth of the loan is compounded monthly, and the monthly payment is determined by dividing the entire compounded cost of the loan by the total number of months. So the first monthly payment will be x. The following month you will pay (x + x * r/12), and in the third month, x + (2x + x* r/12) *r/12 = x ( 1 + r/12)2. So the sum of the payments after p months
= x + x (1 + r/12) + x(1 + r/12)2 + x(1 + r/12)3 + x(1 + r/12)4 + x(1 + r/12)5 + x(1 + r/12)6 + ... x(1 + r/12)p-1
= x(1 + (1 + r/12) + (1 + r/12)2 + (1 + r/12)3 + (1 + r/12)4 + (1 + r/12)5 + (1 + r/12)6 + ... (1 + r/12)p-1).
This compound interest formula is a geometric progression and geometric progressions can be reduced to the formula:
1 + z + z2 + z3 + . . . + zn = [zn+1 - 1]/[z - 1]
| The Sum of A Geometric Series
If you have any doubts about this formula. Let's show that the geometric formula works:
The definition of a geometric progression can also be viewed by saying that the following: The next sum in the geometric progression can be defined by the taking the previous sum, multiplying all parts of the series by the factor and then adding 1 to it.
Another words: f(n) = 1 + z + z2 + z3 + . . . + zn
f(n+1) = 1 + z (1 + z + z2 + z3 + . . . + zn) = 1 + z f(n)
Also (more obviously), the next sum in the progression equals the previous sum plus the next highest factor
f(n+1) = f(n) + zn+1
Taking the two equations for f(n+1) and using substitution:
1 + zf(n) = f(n) + zn+1
solving for f(n):
f(n) = (zn+1 - 1)/(z-1) |
So plugging our geometric formula for mortgages into the geometric progression equation gives us:
Total Mortgage = x * ((1 + r/12((p-1) + 1) - 1)/(1 + r/12 - 1))
Reducing the equation:
Total Mortgage = x * ((1 + r/12)p - 1)/( r/12)
= 12x / r * ((1 + r/12)p - 1)
The actual value of the total mortgage is the initial loan value compounded over the period of time the loan is paid:
Total Mortgage = (Loan Value) * (1 + r/12) p
Substituting the formula for the total mortgage into the equation, The final formula for a mortgage (known as the amortization equation) is shown below:
(Loan Value) * (1 + r/12) p = 12x / r * ((1 + r/12)p - 1)
Let's plug this formula in for our $100,000 loan at 6% over 30 years (360 months)
100,000 (1 + .06/12) 360 = 12x / .06 * ((1 + .06/12)360 - 1). = 200x * 5.02257 = 1004.5x
602,257.52 = 1004.5x
Now solve for x to get our monthly payment.
x = 602,257.52/1004.5 = $599.56
In other words, you would need to pay $599.56 monthly for 30 years to pay off a $100,000 loan at 6%. (This is not including the yearly property tax and the home owner's insurance).
The Design
The Mortgage Calculator consists of just two classes: a Windows Form for accepting input and for doing the calculation, and a ThousandsTextBox that overrides the TextBox control class in order to allow the user to type in numbers and handle the comma separator for the thousands place. The ThousandsTextBox also has a property CurrentValue that allows you to translate between the double and string value inside the text box.
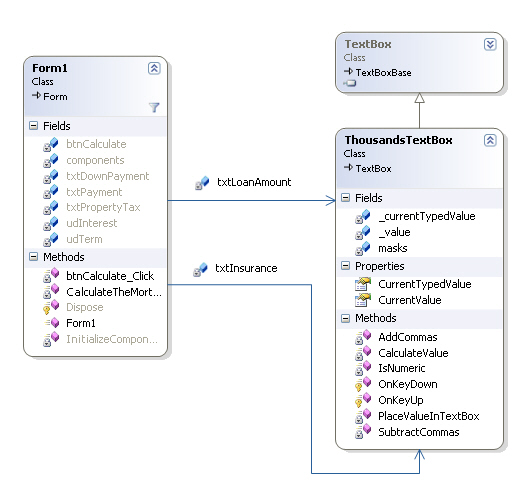
Figure 2 - UML Class Diagram for the Mortgage Calculator
The Code
The C# code for calculating the mortgage takes all the input fields from the NumericUpDown controls and the ThousandTextBox controls and plugs them into the mortgage formula. The calculator also takes into account payments for both the property tax and the home owner's insurance. Listing 1 shows the calculation of the mortgage performed inside the Form.
Listing 1 - Calculating the mortgage using the compound interest formula
| private void CalculateTheMortgage()
{
// (Loan Value) * (1 + r/12) ^ p = (12x / r) * ((1 + r/12)^p - 1)
// payment = (((Loan Value) * (1 + r/12) ^ p) * r)/ (12 * ((1 + r/12)^p - 1)));
double loanAmount = (double)txtLoanAmount.CurrentValue; // price of total mortgage before down payment
double taxesPerYear = (double)txtPropertyTax.CurrentValue; // this will divided by 12 and added to the monthly payment
double downPayment = (double)txtDownPayment.CurrentValue; // down payment will be subtracted from the loan
double interestRate = (double)udInterest.Value / 100; // calculate interest from 100%
double termOfLoan = (double)(udTerm.Value * 12); // monthly term
double propertyTax = (double)txtPropertyTax.CurrentValue;
double insurance = (double)txtInsurance.CurrentValue;
// plug the values from the input into the mortgage formula
double payment = (loanAmount - downPayment) * (Math.Pow((1 + interestRate/12), termOfLoan) * interestRate)/(12 * (Math.Pow((1+interestRate/12), termOfLoan) - 1));
// add on a monthly property tax and insurance
payment = payment + (propertyTax + insurance) / 12;
// place the monthly payment calculated into the output text field
txtPayment.CurrentValue = (int)payment;
} |
The Thousand Text Box
The ThousandsTextBox is basically a simple version of a homemade masked text box control that demonstrates how one might handle placing commas in a text box as you type. Initially I tried using the masked text box that comes with Visual Studio, but this proved cumbersome from a user's perspective, so I decided to whip up my own control. The key to creating a masked textbox control is to override the OnKeyDown event so that you can intercept the key strokes and determine what the contents of the control should be before the control key information is displayed.
The OnKeyDown event handler in our ThousandsTextBox first checks to see if a number (or backspace) was typed. If it wasn't a number, the input is suppressed and the handler returns. If the character is a number, the commas are stripped from the control, the character is appended, and the commas are placed back into the control according to a mask in the mask array. We chose the proper mask for our ThousandsTextBox by 1) counting the number of characters of the text inside the textbox (ignoring the commas) 2)applying the resulting count to the index of the mask array. For example, if our value is 10000, then since 10000 has 5 characters we would pick the 5th array element (or "##,###") to use as our mask.
Listing 2 - Overriding the OnKeyDown Handler in the ThousandsTextBox
| string[] masks = new string[] { "#", "##", "###", "#,###", "##,###", "###,###", "#,###,###", "##,###,###", "###,###,###", "#,###,###,###" };
protected override void OnKeyDown(KeyEventArgs e)
{
// get the character that was pressed
char keycode = (char)e.KeyValue;
// determine if the character pressed was numeric or
// if the character would go beyond the limit of the largest mask
if ((!IsNumeric(keycode)) || Text.Length >= masks[masks.Length - 1].Length)
{
// if it's not numeric, don't try to handle it
// and suppress the character so it won't be displayed
e.Handled = true;
e.SuppressKeyPress = true;
if (keycode != '\b')
{
// if it's a backspace, we still want to react to the keypress, otherwise return
return;
}
}
// add the character to the final string if its not a backspace
if (keycode != '\b')
{
Text += keycode;
}
// take out all the commas, to get the raw number
_currentTypedValue = SubtractCommas(Text);
// handle the backspace by removing the digit at the end of the string
if (keycode == '\b') // take out a character
{
if (SelectionStart >= 0)
{
if (_currentTypedValue.Length > 0)
{
_currentTypedValue = _currentTypedValue.Remove(_currentTypedValue.Length - 1, 1);
}
}
}
// Put the commas back in the number string using the
// mask that matches the number string length
_currentTypedValue = AddCommas(_currentTypedValue);
// Assign the Text property of the edit box to the
// comma decorated string
Text = _currentTypedValue;
if (Text.Length > 0)
{
// select the last character
Select(Text.Length - 1, 1);
}
// mark that we have just handled the key press event
e.Handled = true;
} |
Conclusion
Mortgages can be a daunting concept for first time home buyers. The real estate market is filled with costs that will make your head spin. Sometimes it is good idea to plug the values into a program or spreadsheet so that you can get an accurate picture of your expenses. This mortgage calculator can help you determine a ball park figure of the cash you'll need to shell out on a monthly basis if you are considering a long term home mortgage. So use it wisely to help you determine your .NET costs and to help you C a Sharp and bright future :-).