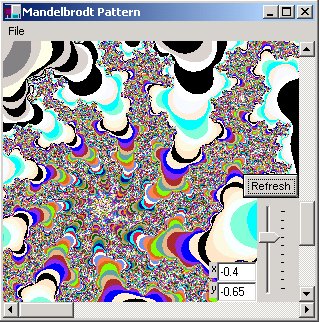
This program illustrates the use of the algorithm to create the Mandelbrodt set. The formula is an iterative one and is plotted in the complex plane (x, yi). The way to generate a Mandelbrodt set is with the following formula:
Z(n+1) = Z(n)2 + Z(0)
The first point, Z(0), is also the location of the pixel on the imaginary plane. The way to choose the color of the pixel point to plot is to count the number of iterations it takes for | Z(n) | to be greater than 2 (|Z(n)| is calculated by taking the modulus of the complex number (x2 + yi2)1/2 ). We put a limit of 150 on the number of iterations in our program in the cases where Z(n) converges.
We have also added to our program a horizontal scroll bar, a vertical scrollbar, and a slider control for scaling. Also there are two textboxes for adjusting any additional offset you wish in the plane. Note that drawing is done in a thread so you can interrupt drawing if you don't like the picture by hitting s for stop. The refresh button will restart drawing at the scrollbar and scaling locations you set. The File Menu allows you to print and print preview the design on the screen. You can also resize the Form to look at a larger area of the pattern.
Below is the code for plotting the Mandelbrodt set:
/// <summary>
/// DrawAll is performed in a thread
/// It contains the actual algorithm for determining pixel color
/// on the complex plane
/// It also does the drawing
/// </summary>
public void DrawAll(Graphics g)
{
// create a complex # z
Complex Z = new Complex( 0.0, -0.0);
Rectangle rect = this.ClientRectangle;
// create a complex # z
Complex Z = new Complex( 0.0, -0.0);
Rectangle rect = this.ClientRectangle;
// iterate over the area in the complex plane indicated by the Scaling and Offset
// i is the real axis, j is the complex axis
for (double i = -rect.Width/2; i < rect.Width/2 ; i++)
{
for (double j = -rect.Height/2; j < rect.Height/2; j++)
{
// Normalize Z and adjust for Scaling and Offset
Z.real = (i/((double)InitialSize)) * Scaling + Offset.real;
Z.imag = (j/((double)InitialSize)) * Scaling + Offset.imag;
// C is the Z(0) of the formula based on the pixel position
// We've also added a ManualOffset from the text boxes on the screen
C.real = Z.real + ManualOffsetX;
C.imag = Z.imag + ManualOffsetY;
// initialize the interation counter
int iteration = 0;
// iterate a maximum of 150 times and break
// out if or when |Z| > 2
for (int k = 1; k < 150; k++)
{
// iterative mandelbrodt formula
Z = (Z*Z) + C;
// if modulus of Z > 2, break out of the loop
// and remember the current iteration to choose the color
if (Math.Abs(Z.Amplitude()) > 2.0)
{
iteration = k;
break;
}
}
// draw the point on the complex plain and choose the color based on the iteration
// the color is picked by casting the iteration to a KnownColor enumeration
// I suspect the colors would look better if they were chosen based on some formula over RGB
DrawComplexPoint(gGraphics, ((int)i) + (rect.Width/2), ((int)j) + (rect.Height/2), iteration);
}
}
// change the cursor back to an arrow, we are done drawing
this.Cursor = Cursors.Arrow;
}
There still needs to be a few improvements to the scrolling. It would also be a nice if you could point to a region on the plane and zoom into it. I've been having fun printing some cool graphics though. Download and enjoy!