I just finished reading Michael Crichton's Science Fiction/Horror book Prey and I admit I could not put the book down. The book combines the concepts of the Swarm Algorithm with nanotechnology to create a very frightening concept( I won't go into detail, because I don't want to spoil it for the reader). What is so fascinating about some of Michael Crichton's books is that he mixes and explains real state of the art technology with his storyline. He also presents possible inventions and breakthroughs in the current technology to fill the implausible gaps of the story, the mark of a great science fiction writer. After reading the book, I decided to go out on the web and see what has been done with modeling swarms in the computer world. (There is also an impressive bibliography of papers and texts in the back of Prey pointing to references on artificial life, genetic algorithms, and intelligent agents).

Figure 1 - The Swarm Algorithm Coming to Life
In my short-lived research I found an article that embeds a java app simulating swarm behavior written by Alex Vulliamy and Jeff Cragg. Rather than reinvent the wheel, I took this code and translated it into C# to demonstrate the swarm behavior in a Windows Form using GDI+. The algorithm is exactly the same and also a fairly simple one. In order to understand the algorithm let's first talk a little bit about the social behavior of birds in a flock.
I think we can all agree that birds are not exactly the brightest of animals (hence the term "bird-brain"), so how do they know how to fly so organized in a flock? (This question was pointed out in Crichton's book by the way). The way each individual bird determines how he will fly is simply by seeing where its neighbors are in the flock and adjusting its velocity so as not to collide with the bird in front of it. If you put this series of simple behavior together for all birds, the combined result is birds flying in a nice formation. Another words, its not like these birds got together and said, "Hey let's form a big V, like the cheerleaders for Villanova". No, they simply rely on their neighbor to determine their behavior.
So how does this all pan out as a mathematical algorithm? Well, let's say you are a bee. You would then obey the following rules (according to this particular program):
-
Accelerate towards your two closest neighbors.
-
If you get too close, repel your neighbor.
-
Don't ever exceed your maximum speed (after all you are a bee, not a rocket ship).
-
If you hit a wall, reverse your direction.
-
Try to have a tendency to accelerate towards the center of the enclosed space
-
Check the proximity of your neighbors' neighbors. If they are closer, follow them.
-
Every once in a while randomly choose some other set of neighbors to follow.
That's all there is too using your limited intelligence as a bee. Just follow a few simple rules and the combined result produces an interesting effect shown in figure 2.

Figure 2 - Simulated bee swarm following each other around
The "bees" seem to follow each other around in a group in a 3D mass not unlike a real bee swarm. (Its hard to tell much from the picture because you can't really see the motion, so you'll just have to run the simulation ;-)
Below is the UML design of our simple Swarm Simulation. It consists of only two classes: the Form and Swarm3D. The Form displays the simulation, and the Swarm3D class contains the Simulation thread, simulation rules, and the code to draw the bees inside the form:
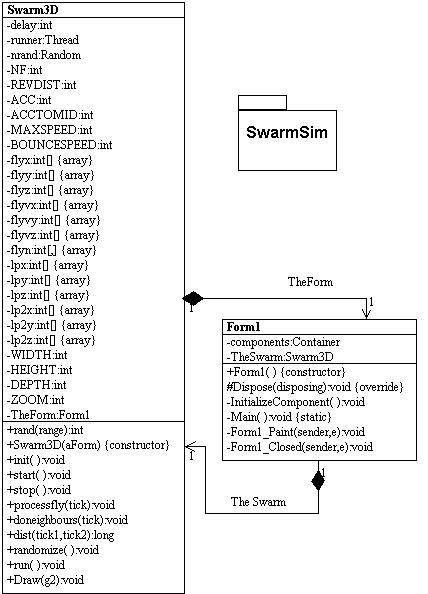
Figure 3 - UML Design of Simulation Program reversed using WithClass 2000
The architecture goes something like this: The Form constructs an instance of the Swarm3D class and calls start to kick off the swarm simulation thread. Each time the simulation needs to update the screen with new swarm positions, it invalidates the form so it will repaint itself. When the form repaints, it calls the Draw method of the Swarm3D class.
The swarm algorithm is implemented in the run routine of the Swarm3D class shown in Listing 1 below. The listing follows all of the rules we have listed above. Most of the rules (1-5), such as follow your neighbor, avoid colliding with your neighbor, don't exceed maximum speed, and bounce off the walls are handled in the processfly method. doneighbors checks the proximity of the neighbors' neighbors and applies rule # 6. Rule #7 is handled by the randomize method in order to pick new neighbors every once in a while.
Listing 1 - run method simulating the swarm:
public
void run()
{
int c=0;
// continue with the simulation as long as the thread is running
while (Thread.CurrentThread ==runner)
{
for (int i=0;i<NF;i++)
{
// determine if there are closer neighbors (rule #6)
doneighbours(i);
// alter the velocity vectors of the bees according to the algorithm rules (Rules #1-5)
processfly(i);
}
// increment a counter to track the number of frames
c++;
// every once in a while, change the neighbors around to new random neighbors (rule # 7)
if (rand(20)==0) randomize();
try
{
// Delay the new positioning so the simulation is not too fast for the eye
Thread.Sleep(delay);
}
catch (Exception e)
{
}
// Force the form to redraw the new positions of the bee
TheForm.Invalidate();
}
}
The most interesting method as it applies to our swarm algorithm is the processfly method which invokes a majority of the rules (1-5) shown in Listing 2. In this method, we compute a 3D Velocity vector for the bee based on the swarm rules. Then we add the velocity vector to the 3D position vector of the bee to determine its new position in the swarm. Note that we need to check each of the x,y, and z directions vectors against the rules of the algorithm.
Listing 2 - processfly method applying rules 1 - 4
public
void processfly(int tick)
{
// rev determines whether the neighbour attracts or repels, ACC is the acceleration amount
// lpx & lpy are the last positions of the bee for drawing purposes.
// REVDIST is the minimum distance squared that the flies can get to without repelling
// tick is the bee number being processed. flyvx&y are the velocities in x and y directions
// ACCTOMID is the acceleration towards the middle to attempt to keep the flies in the
// middle of the display.
lpx[tick]=flyx[tick];
lpy[tick]=flyy[tick];
lpz[tick]=flyz[tick];
int rev=1;
// check the distance between the bee and its neighbors
// use the Acceleration constant and relationship to neighbors to
// compute the velocity of the bee.
// reduce the velocity vector if the bee is getting too close to the neighbor
// if the neighbor is closer than the minimum distance allowed, reverse the direction of the bee
if (dist(tick,flyn[tick,0])<REVDIST)
rev=-1;
// Accelerate towards your neighbor (rule #1)
// if you get too close, repel your neighbor (rule #2)
if (flyx[tick]<flyx[flyn[tick,0]])
flyvx[tick]+=ACC*rev;
else
flyvx[tick]-=ACC*rev;
if (flyy[tick]<flyy[flyn[tick,0]])
flyvy[tick]+=ACC*rev;
else
flyvy[tick]-=ACC*rev;
if (flyz[tick]<flyz[flyn[tick,0]])
flyvz[tick]+=ACC*rev;
else
flyvz[tick]-=ACC*rev;
rev=1;
if (dist(tick,flyn[tick,1])<REVDIST)
rev=-1;
if (flyx[tick]<flyx[flyn[tick,1]])
flyvx[tick]+=ACC*rev;
else
flyvx[tick]-=ACC*rev;
if (flyy[tick]<flyy[flyn[tick,1]])
flyvy[tick]+=ACC*rev;
else
flyvy[tick]-=ACC*rev;
if (flyz[tick]<flyz[flyn[tick,1]])
flyvz[tick]+=ACC*rev;
else
flyvz[tick]-=ACC*rev;
// make sure that the bee's velocity never exceeds the maximum speed (Rule #3)
if (flyvx[tick]>MAXSPEED) flyvx[tick]=MAXSPEED;
if (flyvx[tick]<-MAXSPEED) flyvx[tick]=-MAXSPEED;
if (flyvy[tick]>MAXSPEED) flyvy[tick]=MAXSPEED;
if (flyvy[tick]<-MAXSPEED) flyvy[tick]=-MAXSPEED;
if (flyvz[tick]>MAXSPEED) flyvz[tick]=MAXSPEED;
if (flyvz[tick]<-MAXSPEED) flyvz[tick]=-MAXSPEED;
// make sure the bee's position never exceeds the boundaries of the cube (Rule #4)
if (flyx[tick]<0) flyvx[tick]=BOUNCESPEED;
if (flyx[tick]>WIDTH*100) flyvx[tick]=-BOUNCESPEED;
if (flyy[tick]<0) flyvy[tick]=BOUNCESPEED;
if (flyy[tick]>HEIGHT*100) flyvy[tick]=-BOUNCESPEED;
if (flyz[tick]<0) flyvz[tick]=BOUNCESPEED;
if (flyz[tick]>DEPTH*100) flyvz[tick]=-BOUNCESPEED;
// make sure the bees tend to travel towards the middle of the cube (Rule #5)
if (flyx[tick]<WIDTH*50) flyvx[tick]+=ACCTOMID;
if (flyx[tick]>WIDTH*50) flyvx[tick]-=ACCTOMID;
if (flyy[tick]<HEIGHT*50) flyvy[tick]+=ACCTOMID;
if (flyy[tick]>HEIGHT*50) flyvy[tick]-=ACCTOMID;
if (flyz[tick]<DEPTH*50) flyvz[tick]+=ACCTOMID;
if (flyz[tick]>DEPTH*50) flyvz[tick]-=ACCTOMID;
// compute the new bee position based on the computed velocity
flyx[tick]+=flyvx[tick];
flyy[tick]+=flyvy[tick];
flyz[tick]+=flyvz[tick];
}
Conclusion
The swarm algorithm may seem like a novelty, but it is actually useful for optimization problems in physics, economics, and chemistry. You can add a genetic algorithm to the swarming algorithm to produce emergent behaviors or generate "new rules" to follow in order to achieve a particular goal. Just make sure the goal doesn't exceed its boundary's as they did in Michael Crichton's unfolding tale.
References
Michael Crichton's Prey on Amazon
Simulating Social Behavior
Alex Vulliamy's Home Page
Ariel Dolan's ALife Experiments
AI Depot