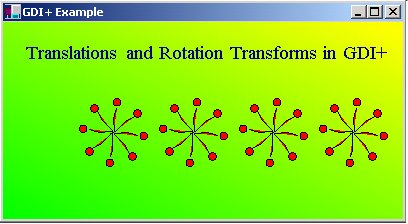
The documentation on transforms in GDI+ is a little sparse in MSDN right now, so I decided to right an article on an sample program on how to use them. Transforms are matrices that allow you to rotate and translate your graphics shapes. In this example we are going to rotate a very powerful element in C# called the GraphicsPath. This element allows you to draw virtually any complex shape using curves, lines, rectangles, ellipses, text, etc. You can then treat the Graphics path as a unit and then move it or rotate it using the Transforms.
Below is the code for creating our Graphics Path balloon:
// create a graphics path
GraphicsPath gp = new GraphicsPath();
// add a squiggly curve to it to look like a balloon string
gp.AddBezier(110, 110, 110, 115, 120, 115, 125, 130);
// add an ellipse to the end of it to look like a balloon
gp.AddEllipse(125,130, 8,8);
// save a copy of the graphics path so we can reset
// each time we rotate it.
GraphicsPath gpOld = new GraphicsPath();
gpOld = (GraphicsPath)gp.Clone();
Now that we have our red balloon we can construct a routine that will translate it and rotate it. In order to rotate the GraphicsPath, we need to first construct an identity matrix. The matrix class actually consists of 2 matrices. There is a 2x2 matrix which is used for the rotation. There is also a 2 x 1 matrix which serves as the translation matrix. The 2x2 matrix is multiplied by the initial point to transform the point for rotation and the 2x1 matrix is added to the initial point to move it for translation. The example below is a rotation at 0 degrees (or no rotation).
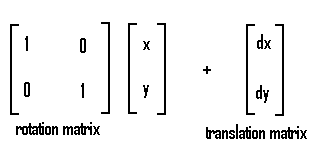
You can combine both rotation and translation matrixes into one and use it to transform a single point as shown below:
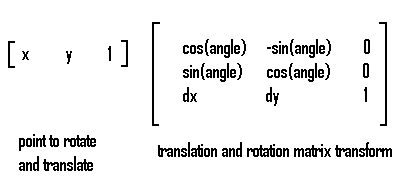
The Matrix class encapsulates all the sine and cosine functions needed to perform rotation and translation through a few key methods in the matrix class. To obtain the rotation matrix at a particular angle, you use the RotateAt method of the matrix which takes an angle in degrees and the point to rotate around. To obtain a translation matrix, you use the Translate method of the matrix class and pass it the dx and dy amount you want the translation offset to be. When we finally want to rotate our GraphicsPath, we call the GraphicPath's Transform method using the transformed matrix. Below is the code for our balloon design. Here we actually used two separate matrices, one for rotation and one for translation so you can clearly see how each is used:
Matrix RotationTransform =
new Matrix(1, 0, 0, 1, 0, 0); // rotation matrix
Matrix TranslationTransform = new Matrix(1, 0, 0, 1, 0, 0); // translation matrix
PointF TheRotationPoint = new PointF(110.0f, 110.0f); // rotation point
// cycle through 4 translated balloon wheel patterns
for (int i = 0; i < 4; i++)
{
// cycle through 360 degrees and draw a balloon at each 45 degree angle
for (float f = 0.0f; f < 359.0; f += (float)45.0)
{
// use the translation matrix to translate the graphics path
// to the right
gp.Transform(TranslationTransform);
// rotate the rotation transformation matrix f degrees around TheRotationPoint
RotationTransform.RotateAt(f, TheRotationPoint);
//Call the Transform method of the Graphics Path in order to multiply it by the rotation matrix and rotate the balloon
gp.Transform(RotationTransform);
// Fill the balloon with a red colored brush
g.FillPath(Brushes.Red, gp);
// Draw the balloon with a black pen
g.DrawPath(Pens.Black, gp);
// reset the transformation matrix
RotationTransform.Dispose();
RotationTransform = new Matrix(1, 0, 0, 1, 0, 0);
// get the original graphics path for our rotation and translation reference
gp = (GraphicsPath)gpOld.Clone();
}
//move the translation matrix by an offset. When the matrix is then
// used in the transform method(above), it causes the balloon wheel to
// be drawn to the right (translation in the positive X direction)
TranslationTransform.Translate(offsetValue, 0);
// We also need to translate the point that we rotate around
TheRotationPoint.X = TheRotationPoint.X + offsetValue;
}
The Matrix also let's you transform your Graphics path in other ways by using the Scale method in the matrix or the Shear Matrix method. Look for future articles in the Graphics section to help you get a head start for using GDI+.