Figure 1 - Biological Chromosomes were the incentive for Genetic Algorithms
One of the more interesting developments that has come out of the Artificial Intelligence world is the invention of Genetic Algorithms. Surprisingly enough Genetic Algorithms have been around before the dawn of man. The idea of using Genetic Algorithms has emerged from the observation of life and evolution. Life reproduces and evolves by exchanging DNA information to produce a mixture of traits. Those organisms possessing the traits geared for survival in the given environment produce the next generation. This generation will contain some organisms that may be better geared for survival in the given environment. After many generations, the newer generations will be the most equipped to survive. Mutations in every generation may also help or hinder an organism in its survival in the environment.
Although this discussion sounds like it has nothing to do with Computer Science, it actually is exactly how Genetic Algorithms work. Genetic Algorithms have a few main components described below:
- Genome A sequence of values (could be characters, floats, ints, structures, or even classes)
- Generation Genomes existing at a specific point in time during the algorithm
- Population A group of Genomes in the current Generation
A set of Genomes in a population undergo a series of steps to produce the next generation. Below are some terms used to describe these steps:
- Fitness A number describing the probability for a Genome to survive and reproduce.
- Crossover When two Genomes exchange pieces of their data with one another.
- Mutation When a piece of data in a Genome is altered randomly.
- Reproduce When a Genome copies itself into the next generation
There are actually many variations of Genetic Algorithms. The one we will talk about is known as the Simple Genetic Algorithm and this one is fairly straightforward. The steps of the algorithm are as follows:
- Produce an initial generation of Genomes using a random number generator.
- Determine the fitness of all of the Genomes.
- Determine which Genomes are allowed to reproduce.
- Crossover the Genome pairs in the allowable population.
- Pick the 2 fittest Genomes of the 2 parents and 2 children resulting from the crossover and add them to the next generation.
- Produce random mutations through the next generation population.
- Calculate the next generations fitness and loop back to step 3.
In creating our Genetic Algorithm class design we tried to make it somewhat generalized. Below is the UML class diagram describing the Genetic Algorithm classes. The two main Genetic Algorithm classes (Population and Genome) consist of the terms we described above in the algorithm. Genome has methods such as Crossover, CalculateFitness, and Mutate to execute the main events occuring in the life of a Genome. Population has functions NextGeneration to produce the next generation and WriteNextGeneration to write the next generation to the Console.
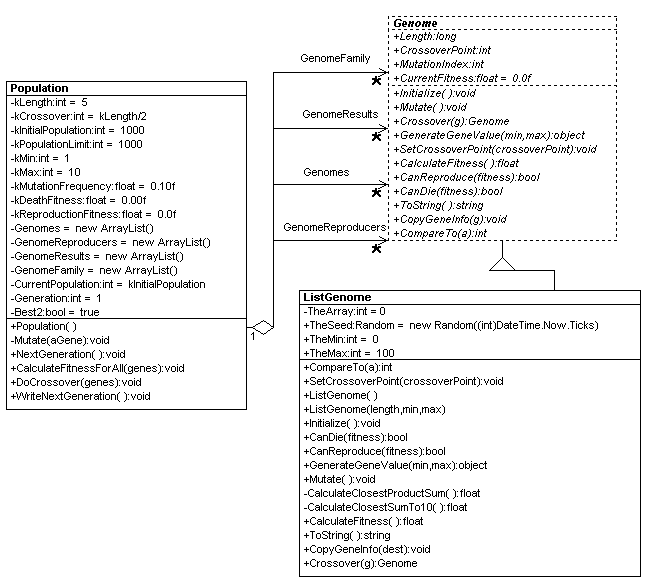
Figure 2 - Genetic Algorithm UML Design reverse engineered using the WithClass 2000 UML Tool
Note that the Genome class is abstract. This way you can inherit other Genome types from it that suit the needs of your problem. The ListGenome subclass is an array of 5 integers because the problem we chose to solve in our fitness function is to find a specific set of 5 integers.
Here is the Problem we want to solve:
What 5 numbers with values 1-10 will produce a product equal to its sum? (Numbers are allowed to repeat.)
The hardest part of executing a genetic algorithm is coming up with a fitness function once the appropriate classes are in place. Also you sometimes need to adjust some of the population constants such as initial population size, mutation frequency, and crossover fitness to help in balancing convergence and diversity in the solution population.
Below is the main function executing the algorithm through 100 generations and writing them to the console.
Listing 1 - Executing the Genetic Algorithm from the Main method
static
void Main(string[] args)
{
Population TestPopulation = new Population();
TestPopulation.WriteNextGeneration();
for (int i = 0; i < 100; i++)
{
TestPopulation.NextGeneration();
TestPopulation.WriteNextGeneration();
}
Console.ReadLine();
}
The constructor of the Population automatically creates the initial set of Genomes. By repeatedly calling the NextGeneration method, you execute the algorithm to produce the next generation. Eventually the population converges to the highest fitness scores. Below is the method used to calculate the fitness of the Genome in the ListGenome class. Note that if the product of the sequence of 5 numbers in the Genome equals the sum of the 5 numbers in the Genome, then the fitness is automatically 1.0 (100%), otherwise we need to come up with a way to assign a fitness if this is not true. The numbers that have products and sums that almost match should have greater fitnesses than those with products and sums far apart. We do this by taking the reciprocal of the difference between the product and sum of the numbers in the genome. Then we make sure the fitness is a positive value by taking the absolute value of the fitness. For products and sums that are only one apart, this produces a fitness of 1.0, so we needed to subtract a little offset to show that this isn't a perfect fitness. Below is the listing for calculating the fitness of the Genome for our problem.
Listing 2 - Calculating the Fitness of a Genome for the product-sum equivalency problem
// This fitness function calculates the closest product sum
private float CalculateClosestProductSum()
{
// fitness for a perfect number
float sum = 0.0f;
float product = 1.0f;
for (int i = 0; i < Length; i++)
{
sum += (int)TheArray[i];
product *= (int)TheArray[i];
}
if (product == sum)
{
CurrentFitness = 1;
}
else
{
CurrentFitness = Math.Abs(Math.Abs(1.0f/(product - sum)) - 0.02f);
}
return CurrentFitness;
}
The output by the 20th generation looks like the code below. Note that sequences 1 2 2 1 2 and 2 5 1 1 1 have products and sums of 8 and 10 respectively. The reason you are seeing some genes with low fitnesses is because 10% of all genes are mutated in each generation by changing a single number in the sequence. The mutation frequency can be lowered or raised in order to tweak the performance.
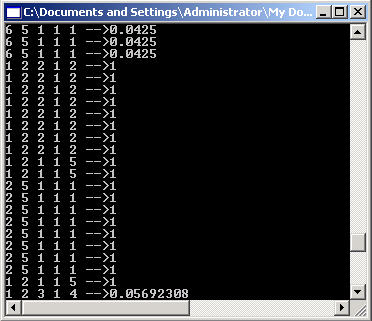
Figure 3 - Output from the 20th generation of the Genetic Algorithm
Conclusion
Genetic algorithms are a great way to solve problems through a trial an error process that progresses very quickly. The success of converging upon a solution depends upon how good your fitness function is, and how well you've tweaked your parameters. Starting with larger populations tends to give you more diversity but takes longer. Increasing mutations helps you find possibilities that may not have occurred in the initial population, but if its too high, its harder for the set to converge. Crossover fitness also can be adjusted to increase or decrease how fast you get to a solution. (It is initially set here at 100%). There are also many other Genetic Algorithms available besides the one we discussed here. Some of them produce subpopulations that grow in tandem. If you find that you are fascinated by the world of GA, a good reference for learning about Genetic Algorithms (at least this is what I've heard) is a book written by David E. Goldberg called Genetic Algorithms in Search, Optimization and Machine Learning. Enjoy manipulating genes in the world of .NET!